State the two factors of comparison when discussing the efficiency of an algorithm.
Time complexity, Space complexity.
Define the time complexity of an algorithm.
How quickly the time it takes to solve a problem increases with the size of input data.
Define the space complexity of an algorithm.
How much space in memory a program uses while solving a problem.
Describe a perfectly efficient algorithm.
One which uses the least space in memory and finishes executing in as little time as possible.
Define Big O Notation.
A measure of time complexity.
What is the time complexity of determining if a number is odd or even.
A single comparison, where time is independent of the size of the inputO(C) = constant.
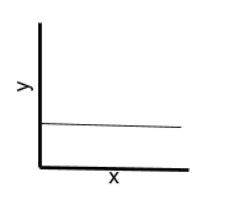
How would one recognise a O(log n) algorithm
Number of items half each iteration (binary search).
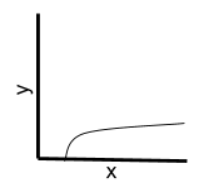
How would one recognise a O(n) algorithm
If each item of the input data must be compared, then the time complexity is linear.
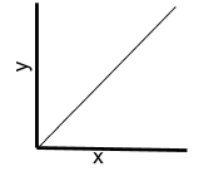
State one linear logarithmic algorithm you have studied.
Merge sort.
A program is designed with a loop within a loop, what is its time complexity?
A loop within a loop signifies a polynomial time solution O(n^2).
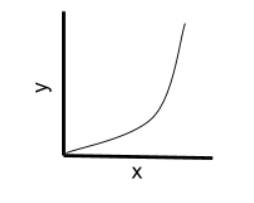
A program is designed with a loop within a loop within a loop, what is its time complexity?
A loop within a loop signifies a polynomial time solution O(n^3).
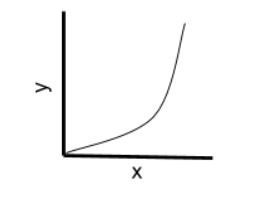
Explain how you could recognise a program to have an exponential time complexity
Often recursion (e.g. recursively calculating numbers within the Fibonacci sequence).
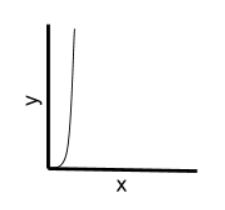
State in order of increasing time complexity the variations of Big-O.
- O(1) - constantO(log n) - logarithmic
- O(n) - linearO(n log n) - linear logarithmic
- O(n^2) - polynomial
- O(2^n) - exponential
- O(n!) - factorial
State the time complexity of intractable problems.
O(2^n) - exponential and O(n!) - factorial
Compare tractable and intractable problems.
- Tractable problems are those within a polynomial time complexity or better, and can be solved within a useful time period.
- Intractable problems are those with exponential or factorial time complexities, and cannot be solved within a useful time period.
Explain how intractable problems may be solved.
Using heuristic methods, a solution is reached which is good enough within a useful time frame.
State the halting problem.
it is impossible to write an algorithm to determine if any input algorithm will finish with a given input.
Explain the importance of the halting problem.
Proves that some problems exist which cannot be solved by computers.