Binary Number System

4.5.4 (19 questions). Public Notes: AQA's A Level Computer Science

How would a computer distinguish between signed and unsigned binary?

It cannot, the computer must be told.

Compare the set of number represented by signed and unsigned binary.

  1. Unsigned binary can only represent positive whole numbers.
  2. Signed binary can only represent both positive and negative whole numbers.

State an expression which describes the range of numbers which n-bit unsigned binary can represent.

0 to (2^n-1)

Boolean Addition Rules

0 + 0 + 0 = ?

0

0 + 0 + 1 = ?

1

0 + 1 + 1 = ?

0 carry 1

1 + 1 + 1 = ?

1 carry 1

Multiplication of two unsigned binary numbers. https://www.youtube.com/watch?v=mAxUtloyk_I
State an expression which describes the range of numbers which b-bit signed binary with twos complement can represent.

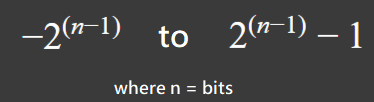
image

Write decimal -5 in signed with twos complement 4-bit binary.

The (leftmost) significant bit is a negative number in the legend.

  • (-)8 4 2 1
  • ---1 0 1 1

(-)8 + 2 + 1 = -5 decimal

State the steps needed to convert an unsigned to two's complement (positive to negative).

Invert every bit, then add 1.

State the steps needed to convert a negative two's complement to (negative to positive)

Subtract 1, then invert bits.

Subtract 12 from 8 in binary.

  1. Convert larger number to negative.

    2. 12 -> -12

  2. Convert both numbers to binary.

    3. -12 in signed two's complement binary is...

    • -16 8 4 2 1
    • __1 0 1 0 0

    8 in signed twos complement binary is...

    • -16 8 4 2 1
    • __0 1 0 0 0

  3. Perform binary addition.

    4. Adding -12 binary to 8 binary.

    • 1 0 1 0 0
    • 0 1 0 0 0
    • 1 1 1 0 0
Checking Answer..
11100 signed two's complement binary in decimal is...
  • -16 8 4 2 1
  • __1 1 1 0 0
-16 + 8 + 4 = -4 decimal
12 - 8 = -4 decimal as well!

Convert 11.75 to fixed point unsigned binary.

  • 16 8 4 2 1 . 0.5 0.25
  • _0 1 1 0 1 . __1 ___1

Convert 01101 . 011 floating point two's complement signed binary to decimal.

  1. Calculate the decimal value of the exponent.

    2. 0 1 1 = 3 decimal

  2. Place a binary point between the first and second digits of the mantissa.

    3. 0 1 1 0 1 → 0 . 1 1 0 1

  3. Move the binary point specified by the decimal exponent.

    4. Three places to the right.
    0 . 1 1 0 1 → 0 1 1 0 . 1

Convert to decimal to check.
  • -8 4 2 1 . 0.5
  • _0 1 1 0 . __1
4 + 2 + 0.5 = 6.5

Convert decimal 14.625 to floating point signed binary.

  1. Convert to fixed point signed binary.

    • -16 8 4 2 1 . 0.5 0.25 0.125
    • __0 1 1 1 0 . __1 ___0 ____1

  2. Normalise.

    1. Decide how far to move point using these two rules.

      1. Positive number so mantissa starts with 01.
      2. If we jad a negative number, mantissa starts with 10.
      01110.101 → 01.110101

    2. Determine exponent using these two rules.

      1. Since we've shifted left 3, exponent is +3.
      2. If we've shifted right 3 exponent is -3.

    3. Convert exponent (-3) to two's complement signed binary.

      • -4 2 1
      • _0 1 1

    4. Concatenate mantissa and exponent like this.

      5. 01.110101 + 011 -> 01110101.011

Answer in floating point signed binary is: 01110101 . 011

The number 14.6 is represented in fixed point binary as 1110.1. Calculate the absolute error.

  1. Convert binary to decimal.

    • 8 4 2 1 . 0.5
    • 1 1 1 0 . __1
    8 + 4 + 2 + 0.5 = 14.5

  2. Absolute error = actual value - given value.

    3. 14.6 - 14.5 = 0.1

Answer: 0.1 decimal absolute error.

The number 12.4 is represented in fixed point binary as 1100.011. Calculate the relative error as a percentage 4 s.f.

  1. Convert binary to decimal.

    • 8 4 2 1 . 0.5 0.25 0.125
    • 1 1 0 0 . __0 ___1 ____1

    8 + 4 + 0.25 + 0.125 = 12.375 decimal

  2. Absolute error = actual value - given value.

    3. 12.4 - 12.375 = 0.025 decimal

  3. Relative error = absolute error / actual value

    4. 0.025 / 12.4 * 100 = 20.16%

Answer: 20.16% 4 s.f.

Compare qualitatively and explain the ranges of fixed point binary and floating point binary

Range of floating point binary > range of fixed point binary, because exponent of floating point binary can be both positive and negative.

Compare qualitatively and explain the ranges of a floating point binary number with (large mantissa and small exponent) and a (small mantissa and a large exponent).

  1. (large mantissa and small exponent) = large range + little precision
  2. (small mantissa and a large exponent) = small range + large precision
Exponent size directly proportional to range.
While mantissa size directly proportional to precision.

State when an underflow error might occur.

Not enough bits to represent very small number.

State when an overflow error might occur.

Not enough bits to represent a large number.